Qi Ye

EMPLOYMENT

●  Director

    Laboratory for Machine Learning and Computational Optimization, South China Normal University, 2016.07 - current

●  Professor

    School of Mathematical Sciences, South China Normal University, 2016.01 - current

● Research Fellow

   Department of Mathematics, Hong Kong Baptist University, 2015.06 - 2015.12

   Joint work with Prof. Dr. Leevan Ling in Radial Basis Functions

● Philip T. Church Postdoctoral Fellow

   Department of Mathematics, Syracuse University, 2012.08 - 2015.05

   Joint work with Prof. Dr. Yuesheng Xu in Machine Learning

● Teaching and Research Assistant

   Department of Applied Mathematics, Illinois Institute of Technology, 2007.08 - 2012.05

RESEARCH INTERESTS

●  Approximation Theory in Data Analysis and Machine Learning

●  Kernel-based Approximation Method, Meshfree Method

●  Support Vector Machine, Artificial Neural Network

●  Nonsmooth Analysis, Convex Analysis

●  Precision Medicine, Intelligent Education

MATHEMATICS IN MACHINE LEARNING

●  Composite optimization algorithms for Sigmoid networks, with Huixiong Chen, Neural Computation, Volume 35, Issue 9, Pages 1543-1565, 2023. (full paper)

●  Splitting method for support vector machine with lower semicontinuous loss, with Mingyu Mo, Pacific Journal of Optimization, Volume 19, Number 4, Pages 689-714, 2023. (full paper)

●  Positive definite multi-kernels for scattered data interpolations, Applied and Computational Harmonic Analysis, Volume 62, Issue 1, Pages 251-260, 2023. (full paper)

●  TGM-Nets: A deep learning framework for enhanced forecasting of tumor growth by integrating imaging and modeling, with Qijing Chen, Weiqi Zhang, He Li, Xiaoning Zheng, Engineering Applications of Artificial Intelligence, Volume 126, Part A, 106867, 2023. (full paper)

●  Analysis of regularized learning for generalized data in Banach spaces, arXiv:2109.03159, Pages 1-36, 2022, submitted.

●  Generalized representer theorems in Banach spaces, with Liren Huang, Chunguang Liu, Lulin Tan, Analysis and Applications, Volume 19, Number 1, Pages 125-146, 2021. (full paper)

●  Support vector machine classifiers by non-Euclidean margins, with Ying Lin, Mathematical Foundations of Computing, Volume 3, Number 4, Pages 279-300, 2020. (full paper)

●  Sparse regularized learning in the reproducing kernel banach spaces with the ℓ1 norm, with Ying Lin, Rongrong Lin, Mathematical Foundations of Computing, Volume 3, Number 3, Pages 205-218, 2020. (full paper)

●  Generalized Mercer kernels and reproducing kernel Banach spaces, with Yuesheng Xu, Memoirs of the American Mathematical Society, Volume 258, Number 1243, Pages 1-122, 2019. (full paper)

●  Application of machine learning methods based on LAZE priors to cancer data -- take the prostate cancer data set for example, with Ying Lin, Journal of South China Normal University, Volume 50, Issue 4, Pages 115-120, 2018 (Chinese). (full paper) 

●  Sparse support vector machines in reproducing kernel Banach spaces, with Zheng Li and Yuesheng Xu, Contemporary Computational Mathematics - A Celebration of the 80th Birthday of Ian Sloan, Editors: Josef Dick, Frances Y. Kuo, Henryk Woźniakowski, Springer, pp 869-887, Cham, 2018. (full paper)

●  Solving support vector machines in reproducing kernel Banach spaces with positive definite functions, with Gregory E. Fasshauer and Fred J. Hickernell, Applied and Computational Harmonic Analysis, Volume 38, Issue 1, Pages 115-139, 2015. (full paper)

●  Solving support vector machines in reproducing kernel Hilbert spaces versus Banach spaces, Approximation Theory XIV: San Antonio 2013, Editors: Gregory E. Fasshauer, Larry L. Schumaker, Springer, pp 377-395, Switzerland, 2014. (full paper)

KERNEL-BASED PROBABILITY MEASURES

● Kernel-based probability measures for generalized interpolations: A deterministic or stochastic problem? Journal of Mathematical Analysis and Applications, Volume 477, Issue 1, Pages 420-436, 2019. (full paper)

● Kernel-based probability measures for interpolations, Applied and Computational Harmonic Analysis, Volume 47, Issue 1, Pages 226-234, 2019. (full paper)

● On meshfree numerical differentiation, with Leevan Ling, Analysis and Applications, Volume 16, Number 5, Pages 717-739, 2018. (full paper)

● Kernel-based approximation methods for partial differential equations: deterministic or stochastic problems? Approximation Theory XV: San Antonio 2016, Editors: Gregory E. Fasshauer, Larry L. Schumaker, Springer, pp 375-398, Cham, 2017. (full paper)

●  Generalizations of kriging methods in spatial data analysis, Meshfree Methods for Partial Differential Equations VIII, Editors: Michael Griebel, Marc Alexander Schweitzer, Springer, pp 145-166, Germany, 2017. (full paper)

●  Optimal designs of positive definite kernels for scattered data approximation, Applied and Computational Harmonic Analysis, Volume 41, Issue 1, Pages 214-236, 2016. (full paper)

●  Kernel-based methods for stochastic partial differential equations, Technical Report of Syracuse University, arXiv:1303.5381v8, Pages 1-54, 2015.

●  Approximation of nonlinear stochastic partial differential equations by a kernel-based collocation method, International Journal of Applied Nonlinear Science, Volume 1, Number 2, Pages 156-172, 2014. (full paper)

●  A kernel-based collocation method for elliptic partial differential equations with random coefficients, with Gregory E. Fasshauer, Monte Carlo and Quasi-Monte Carlo Methods 2012, Editors: Josef Dick, Frances Y. Kuo, Gareth W. Peters, Springer, pp 331-347, Germany, 2013. (full paper)

●  Kernel-based collocation methods versus Galerkin finite element methods for approximating elliptic stochastic partial differential equations, with Gregory E. Fasshauer, Meshfree Methods for Partial Differential Equations VI, Editors: Michael Griebel, Marc Alexander Schweitzer, Springer, pp 155-170, Germany, 2012. (full paper)

●  Approximation of stochastic partial differential equations by a kernel-based collocation method, with Igor Cialenco and Gregory E. Fasshauer, International Journal of Computer Mathematics, Volume 89, Issue 18, Pages 2543-2561, 2012. (full paper)

OTHERS

● Reproducing kernels of Sobolev spaces via a Green kernel approach with differential operators and boundary operators, with Gregory E. Fasshauer, Advances in Computational Mathematics, Volume 38, Issue 4, Pages 891-921, 2013. (full paper)

●  Reproducing kernels of generalized Sobolev spaces via a Green function approach with distributional operators, with Gregory E. Fasshauer, Numerische Mathematik, Volume 119, Number 3, Pages 585-611, 2011. (full paper)

●  Generalized third-order conditions for error bound of proper functions in Banach spaces, with Tan Lulin, Mei Jing, and Huang Liren, Journal of South China Normal University, Volume 50, Issue 5, Pages 106-109, 2018 (Chinese). (full paper) 

PATENTS

●  Medical Image Segmentation Method and System Based on Decoding Layer Loss Recall, with Jiawei Chen, Chihua Fang, Patent #: ZL202310403445.3 (China), Patentee: South China Normal University, 2023.

●  Pancreatic CT Image Registration Method based on Fusion of Multipath Features and Organ Morphology Guidance, with Wenshan Chen, Zhipeng Zhu, Chihua Fang, Patent #: ZL202310755028.5 (China), Patentee: South China Normal University, 2023.

●  Automatic Vascular Segmentation Method for CT Enhanced Images, with Tan Yang, Jieyi Zhou, Yongyi Liu, Chihua Fang, Patent #: ZL202310343462.2 (China), Patentee: South China Normal University, 2023.

●  Medical Image Segmentation Method based on Boosting-Unet Segmentation Network, with Lihui Wen, Jiawei Chen, Chihua Fang, Patent #: ZL202210502143.7 (China), Patentee: South China Normal University, 2022.

●  Medical Image Segmentation Method based on Boosting-Unet Segmentation Network, with Lihui Wen, Jiawei Chen, Chihua Fang, Patent #: HK40067531 (Hong Kong), Patentee: South China Normal University, 2022.

RESEARCH GRANTS

●  The junior program of the National Natural Science Foundation of China, kernel-based approximation methods in data sciences, 2017 - 2019, China

●  The creative program of the major research program of universities at Guangdong, 2018 - 2019, Department of Education of Guangdong Province, China

●  The general program of Natural Science Foundation of Guangdong, 2019 - 2022, Department of Science and Technology of Guangdong Province, China

●  The general program of the National Natural Science Foundation of China, kernel-based approximation methods for generalized data, 2021 - 2024, China

●  The state key program of the National Natural Science Foundation of China, mathematical methods and evolutionary modeling for surgical planning and postoperative evaluation of pancreatic cancer, 2021 - 2024, China

●  The state key program of universities at Guangdong, 2021- 2023, Department of Education of Guangdong Province, China

RESEARCH AWARDS

●  Sigma Xi Award in recognition of the outstanding accomplishments in research and scholarship, 2012, Sigma Xi

●  Karl Menger Student Award, 2012, Illinois Institute of Technology

●  Award in recognition of outstanding efforts and accomplishments on behalf of the SIAM Chapter at the Illinois Institute of Technology in the academic year 2011 - 2012, 2012, SIAM

CONFERENCES ORGANIZATIONS

●  International Conference of Kernel-based Approximation Methods in Data Analysis, May 25-27, 2018, Guangzhou Guangdong, China.

●  International Conference of Kernel-based Approximation Methods in Machine Learning, May 19-21, 2017, Guangzhou Guangdong, China.

●  SIAM Student Chapter Conference 2011 (IIT SIAM 2011): Recent Advances in Computational Science and Statistics, Oct 29-30, 2011, Chicago IL, USA.

COLLOQUIUMS

● Tutorial of kernel-based approximation methods, Tianjin University, Jun 10, 2017, Tianjin, China.

●  Kernel-based approximation methods for partial differential equations: deterministic or stochastic problems, Fudan University, Jan 17, 2017, Shanghai, China.

●  Kernel-based methods for deterministic or stochastic data, Sun Yat-Sen University, May 25, 2015, Guangzhou Guangdong, China.

●  Kernel-based approximation method and its application, Cornell University, Apr 7, 2014, Ithaca NY, USA.

●  Kernel-based approximation method and its application, University of Missouri-St. Louis, Mar 21, 2014, St. Louis MO, USA.

●  Tutorial of meshfree approximation methods, Huazhong University of Science and Technology, Dec 30, 2010, Wuhan Hubei, China.

CONFERENCES

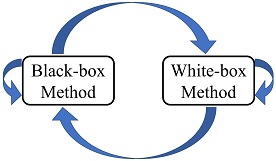
● Machine learning in Banach spaces: a black-box or white-box method? the 10th International Congress on Industrial and Applied Mathematics, Aug 20-25, 2023, Tokyo, Japan.

● Machine learning in Banach spaces: a black-box or white-box method? the 4th International Conference on Frontiers of Mathematics and Artificial Intelligence,  Dec 16-18, 2022, Beijing, China.

● Machine learning in Banach spaces: a black-box or white-box method? the 9th International Consortium of Chinese Mathematicians, Jul 31- Aug 5, 2022, Nanjing, China. 

● Kernel-based probability measures for data analysis: a deterministic or stochastic problem? CSIAM 2018, Sep 13-16, 2018, Chengdu, China.

● Kernel-based approximation methods for generalized interpolations: a deterministic or stochastic problem? the 9th International Conference on Curves and Surfaces, Jun 28-Jul 4, 2018, Arcachon, France. 

●  Kernel-based approximation methods for generalized interpolations: a deterministic or stochastic problem? International Symposium on Computational Harmonic Analysis, Jun 22-24, 2018, Beijing, China.

●  Kernel-based approximation methods for generalized interpolations: a deterministic or stochastic problem? the 2nd Hangzhou Workshop on Harmonic Analysis and Application, Dec 15-17, 2017, Hangzhou, China.

●  Kernel-based approximation methods for partial differential equations: deterministic or stochastic problems, International Conference on Computational Harmonic Analysis 2017, May 24-28, 2017, Shanghai, China.

●  High dimensional data approximation in reproducing kernel Banach space, International Conference on Some Mathematical Approximation Approaches in Data Science, Dec 12-15, 2016, Hangzhou, China.

●  Numerical differentiation by kernel-based probability, International Conference on Information and Computational Science 2016, Aug 2-6, 2016, Dalian, China.

●  Reproducing kernel Banach spaces for nonlinear approximation, the VII Jaen Conference on Approximation Theory, Jul 3-8, 2016, Ubeda Jaen, Spain.

●  Numerical differentiation by kernel-based probability, the 15th International Conference Approximation Theory, May 22-25, 2016, San Antonio, TX, USA.

●  Kernel-based methods for deterministic or stochastic data, the 1st East Asia Symposium of IPIA Programme, Feb 29-Mar 1, 2016, Shenzhen Guangdong, China.

●  Kernel-based methods for deterministic or stochastic data, the 10th Chinese Computational Mathematics Annal Meeting, Sep. 19-22, 2015, Guangzhou, China.

●  Kernel-based methods for deterministic or stochastic data, the 8th International Workshop on Meshfree Methods for Partial Differential Equations, Sep. 7-9, 2015, Bonn, Germany.

●  Kernel-based approximation method for stochastic partial differential equations, International Conference on Spectral and High Order Methods 2014, Jun 23-27, 2014, Salt Lake City UT, USA.

●  Kernel-based approximation method for stochastic partial differential equations, the 5th International Conference on Computational Harmonic Analysis, May 19-23, 2014, Nashville TN, USA.

●  Solving support vector machines in reproducing kernel Banach spaces with Matern functions (poster), Workshop of Low-dimensional Structure in High-dimensional Systems (LDHD), Sep 8-12, 2013, Research Triangle Park NC, USA.

●  Solving stochastic partial differential equations with Levy noises via a kernel-based approximation method, International Conference on Approximation Theory and Applications, May 20-24, 2013, Hong Kong.

●  Solving support vector machines in reproducing kernel Banach spaces with Matern functions, the 14th International Conference Approximation Theory, Apr 7-10, 2013, San Antonio TX, USA.

●  Approximation of stochastic partial differential equations by a kernel-based collocation method, the 3rd New York Conference on Applied Mathematics, Oct 13, 2012, Troy NY, USA.

●  Approximation of stochastic partial differential equations by a kernel-based collocation method, the 10th International Conference on Monte Carlo and Quasi-Monte Carlo Methods, Feb. 13-17, 2012, Sydney, Australia.

●  Approximation of stochastic partial differential equations by a kernel-based collocation method, 2012 Joint Mathematics Meeting: AMS-SIAM Special Session on the Mathematics of Computation, Jan. 4-7, 2012, Boston MA, USA.

●  Approximation of stochastic partial differential equations by a kernel-based collocation method, the 6th International Workshop on Meshfree Methods for Partial Differential Equations, Oct. 4-6, 2011, Bonn, Germany.

●  Approximation of nonlinear partial differential equations by Gaussian processes via Matern functions, the 7th International Congress on Industrial and Applied Mathematics, Jul. 18-22, 2011, Vancouver BC, Canada.

●  Approximation of linear stochastic partial differential equations by Gaussian processes via Matern functions (poster), Recent Advances in the Numerical Approximation of Stochastic Partial Differential Equations, Aug. 9-13, 2010, Chicago IL, USA.

●  Approximation of linear partial differential equations by Gaussian processes via Matern functions, 2010 SIAM Annual Meeting, Jul. 12-16, 2010, Pittsburgh PA, USA.

●  Approximating stable and unstable manifolds of 2D stochastic dynamical systems via reproducing kernels, Midwest Numerical Analysis Day 2010, Apr. 24-25, 2010, Ames IA, USA.

●  A Green function approach to (conditionally) positive definite functions and reproducing kernels of generalized Sobolev spaces, the 13th International Conference on Approximation Theory, Mar. 7-10, 2010, San Antonio TX, USA.

●  Reproducing kernels of generalized Sobolev spaces via a Green function approach, 2009 Joint Midwest Numerical Analysis Day and SIAM Great Lakes Numerical PDEs Spring Conference, Apr. 17-18, 2009, Detroit MI, USA.

ACTIVITY

●  President of Illinois Institute of Technology chapter of SIAM, 2011-2012

MEMBERSHIP

●  Sigma Xi, The Scientific Research Society

●  Foundations of Computational Mathematics

●  China Society for Industrial and Applied Mathematics

●  Society for Computational Mathematics of Guangdong Province

COMPUTER PROGRAMMING SKILL

●  C++, Matlab, Maple, and Mathematica

LANGUAGE

●  English, Cantonese, and Mandarin

NEW AGE OF APPROXIMATION THEORY

●  Approximation in Eye of Horus

from Wikipedia

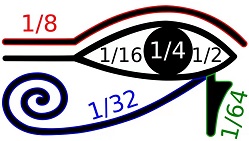
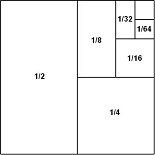
●  Kernel-based Approximation Methods: A Deterministic or Stochastic Problem?

●  Machine Learning in Banach Spaces: A Black-box or White-box Method?

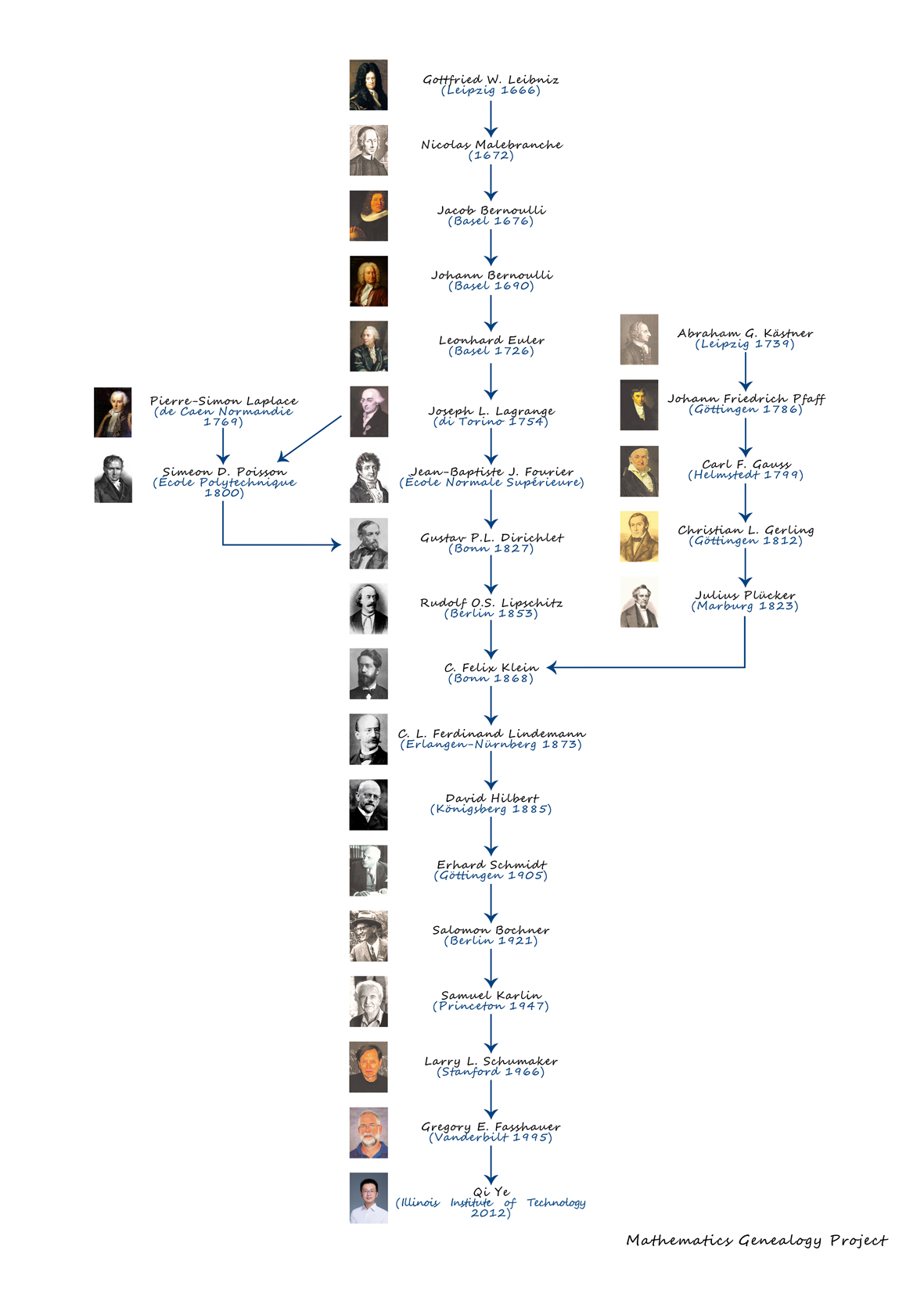
MATH TREE

click to large

TEACHING EXPERIENCE

●  South China Normal University

    1. Statistical learning, Fall 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023

    2. Neural network and deep learning, Spring 2019, 2020, 2021, 2022, 2023

    3. Design and analysis of algorithms, Spring 2017

    4. Advanced mathematics (I), 2015-2016

●  Syracuse University

    1. Numerical methods with programming (MAT 581), Fall 2014

    2. Differential equations and matrix algebra for engineers (MAT 485), Spring 2014, Spring 2013

    3. Calculus III (MAT 397), Fall 2013

    4. The lst course in linear algebra (MAT 331), Spring 2015, Fall 2014

    5. Calculus for the life science (MAT 286), Spring 2014, Fall 2012

●  Illinois Institute of Technology

    1. Teaching assistant of probability and statistics (Math 474/563), applied analysis (Math 500/501), dynamical systems (Math 515), computational mathematics (Math 350/577) and calculus (Math 151/152), duties as tutor, laboratory, grader and sitting in office hours.

    2. Mentor for undergraduate summer research of radial basis functions and time series.

Address: School of Mathematical Sciences, South China Normal University, Guangzhou, Guangdong, China 510631

Phone: +86-20-85216655-8414

Email: yeqi@m.scnu.edu.cn

Webpage: webpage of school

Laboratory: Laboratory for Machine Learning and Computational Optimization